以下为 Jean 学习笔记和习题整理，供学习和参考

# 排序

常见的排序：冒泡、快排、插入、归并、选择、希尔

# 1、冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢 “浮” 到数列的顶端。

	public static void main(String[] args) {

	int arr[] = {7, 5, 3, 2, 4};

	// 冒泡
	for (int i = 0; i < arr.length; i++) {
	// 外层循环，遍历次数
	for (int j = 0; j < arr.length - i - 1; j++) {
	// 内层循环，升序（如果前一个值比后一个值大，则交换）
	// 内层循环一次，获取一个最大值
	if (arr[j] > arr[j + 1]) {
	int temp = arr[j + 1];
	arr[j + 1] = arr[j];
	arr[j] = temp;
	}
	}
	}
	}

# 2、选择排序（Selection Sort）

a、将第一个值看成最小值，在剩余中选择最小的

b、然后和后续的比较找出最小值和下标

c、交换本次遍历的起始值和最小值

d、说明：每次遍历的时候，将前面找出的最小值，看成一个有序的列表，后面的看成无序的列表，然后每次遍历无序列表找出最小值。

	public static void main(String[] args) {

	int arr[] = {6, 5, 3, 2, 4};

	// 选择
	for (int i = 0; i < arr.length; i++) {
	// 默认第一个是最小的。
	int min = arr[i];
	// 记录最小的下标
	int index = i;
	// 通过与后面的数据进行比较得出，最小值和下标
	for (int j = i + 1; j < arr.length; j++) {
	if (min > arr[j]) {
	min = arr[j];
	index = j;
	}
	}
	// 然后将最小值与本次循环的，开始值交换
	int temp = arr[i];
	arr[i] = min;
	arr[index] = temp;
	// 说明：将 i 前面的数据看成一个排好的队列，i 后面的看成一个无序队列。每次只需要找无需的最小值，做替换
	}
	}

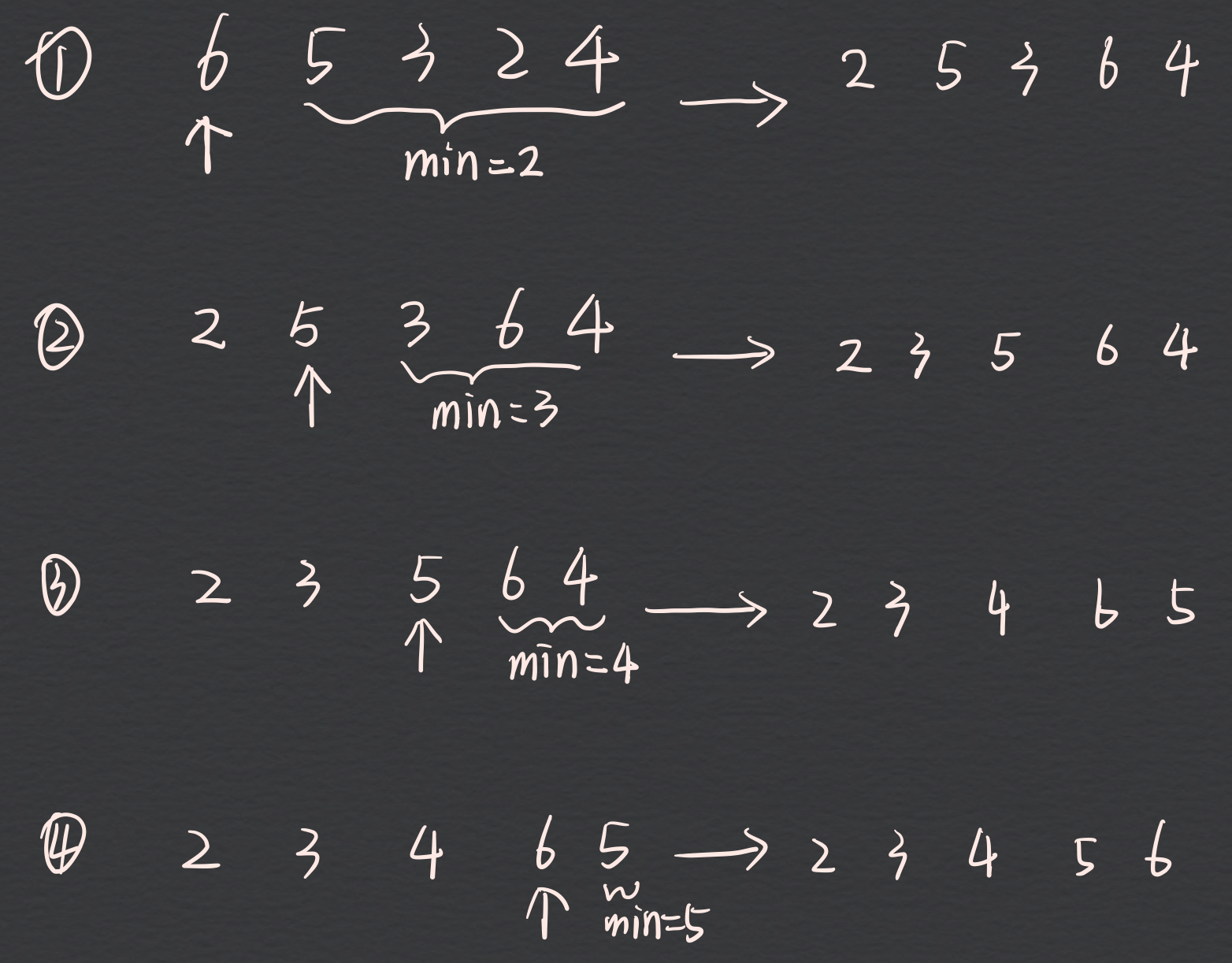
# 3、插入排序（Insertion Sort）

a、默认从第二个数据开始比较，将无序元素插入到有序元素。

b、如果第二个数据比第一个小，则交换。然后在用第三个数据比较，如果比前面小，则插入（狡猾）。否则，退出循环

c、说明：默认将第一数据看成有序列表，后面无序的列表循环每一个数据，如果比前面的数据小则插入（交换）。否则退出。

d、代码实现

	public static void main(String[] args) {

	int arr[] = {7, 5, 3, 2, 4};

	// 插入排序
	for (int i = 1; i < arr.length; i++) {
	// 外层循环，从第二个开始比较
	for (int j = i; j > 0; j--) {
	// 内层循环，与前面排好序的数据比较，如果后面的数据小于前面的则交换
	if (arr[j] < arr[j - 1]) {
	int temp = arr[j - 1];
	arr[j - 1] = arr[j];
	arr[j] = temp;
	} else {
	// 如果不小于，说明插入完毕，退出内层循环
	break;
	}
	}
	}
	}

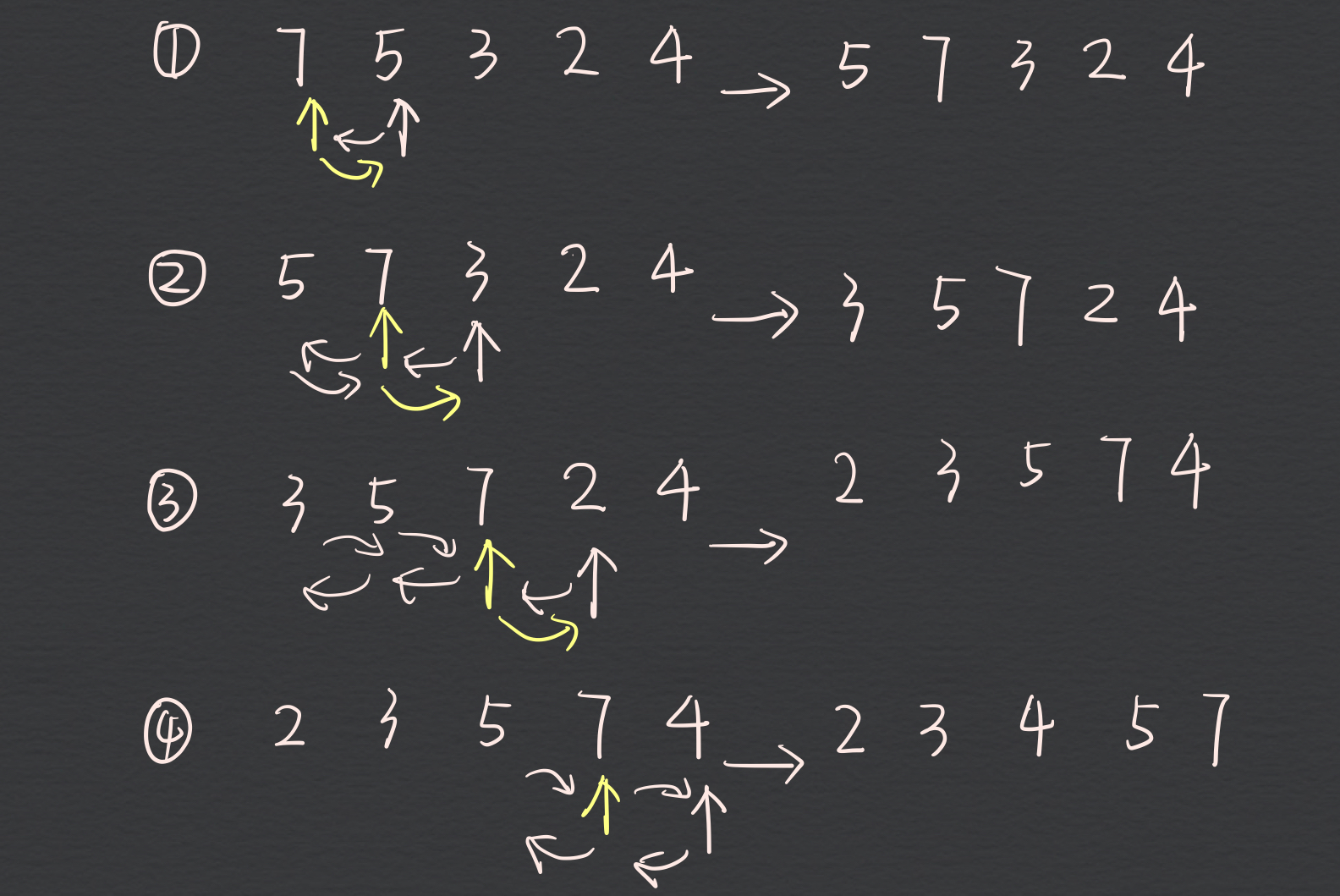
# 4、希尔排序（Shell Sort）

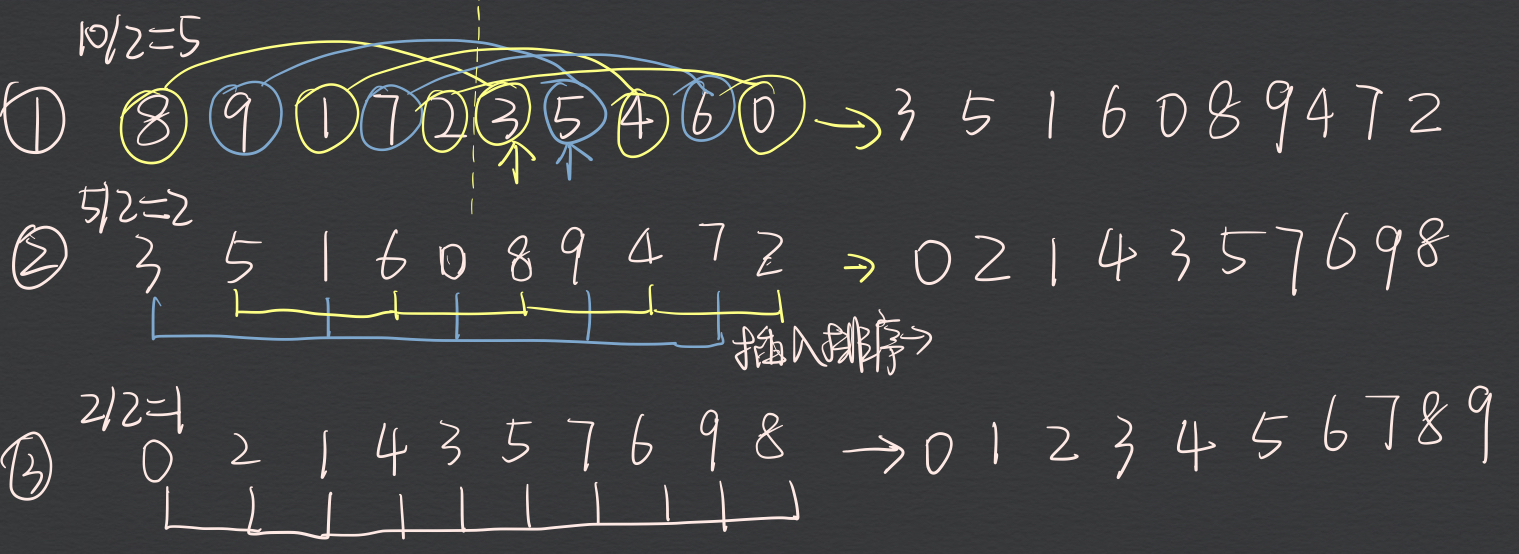
a、基本上和插入排序一样的道理，ps: 插入排序的升级版

b、不一样的地方在于，每次循环的步长，通过减半的方式来实现

c、说明：基本原理和插入排序类似，不一样的地方在于。通过间隔多个数据来进行插入排序。

d、代码实现

	public static void main(String[] args) {

	int arr[] = {8,9,1,7,2,3,5,4,6,0};

	// 希尔排序（插入排序变种版）
	for (int i = arr.length / 2; i > 0; i /= 2) {
	//i 层循环控制步长
	for (int j = i; j < arr.length; j++) {
	//j 控制无序端的起始位置
	for (int k = j; k > 0 && k - i >= 0; k -= i) {
	if (arr[k] < arr[k - i]) {
	int temp = arr[k - i];
	arr[k - i] = arr[k];
	arr[k] = temp;
	} else {
	break;
	}
	}
	}
	//j,k 为插入排序，不过步长为 i
	}
	}

# 5、归并排序（Merge Sort）

a、将列表按照对等的方式进行拆分

b、拆分小最小快的时候，在将最小块按照原来的拆分，进行合并

c、合并的时候，通过左右两块的左边开始比较大小。小的数据放入新的块中

d、说明：简单一点就是先对半拆成最小单位，然后将两半数据合并成一个有序的列表。

e、代码实现

	public static void main(String[] args) {

	int arr[] = {7, 5, 3, 2, 4, 1，6};

	// 归并排序
	int start = 0;
	int end = arr.length - 1;
	mergeSort(arr, start, end);
	}

	public static void mergeSort(int[] arr, int start, int end) {
	// 判断拆分的不为最小单位
	if (end - start > 0) {
	// 再一次拆分，知道拆成一个一个的数据
	mergeSort(arr, start, (start + end) / 2);
	mergeSort(arr, (start + end) / 2 + 1, end);
	// 记录开始 / 结束位置
	int left = start;
	int right = (start + end) / 2 + 1;
	// 记录每个小单位的排序结果
	int index = 0;
	int[] result = new int[end - start + 1];
	// 如果查分后的两块数据，都还存在
	while (left <= (start + end) / 2 && right <= end) {
	// 比较两块数据的大小，然后赋值，并且移动下标
	if (arr[left] <= arr[right]) {
	result[index] = arr[left];
	left++;
	} else {
	result[index] = arr[right];
	right++;
	}
	// 移动单位记录的下标
	index++;
	}
	// 当某一块数据不存在了时
	while (left <= (start + end) / 2 \|\| right <= end) {
	// 直接赋值到记录下标
	if (left <= (start + end) / 2) {
	result[index] = arr[left];
	left++;
	} else {
	result[index] = arr[right];
	right++;
	}
	index++;
	}
	// 最后将新的数据赋值给原来的列表，并且是对应分块后的下标。
	for (int i = start; i <= end; i++) {
	arr[i] = result[i - start];
	}
	}
	}

排序过程：

	5,7,3,2,4,1,6
	5,7,2,3,4,1,6
	2,3,5,7,4,1,6
	2,3,5,7,1,4,6
	2,3,5,7,1,4,6
	1,2,3,4,5,6,7

# 6、快速排序（Quick Sort）

a、确认列表第一个数据为中间值，第一个值看成空缺（低指针空缺）。

b、然后在剩下的队列中，看成有左右两个指针（高低）。

c、开始高指针向左移动，如果遇到小于中间值的数据，则将这个数据赋值到低指针空缺，并且将高指针的数据看成空缺值（高指针空缺）。然后先向右移动一下低指针，并且切换低指针移动。

d、当低指针移动到大于中间值的时候，赋值到高指针空缺的地方。然后先高指针向左移动，并且切换高指针移动。重复 c、d 操作。

e、直到高指针和低指针相等时退出，并且将中间值赋值给对应指针位置。

f、然后将中间值的左右两边看成行的列表，进行快速排序操作。

g、代码实现

	public static void main(String[] args) {
	int arr[] = {7, 5, 3, 2, 4, 1, 8, 9, 6};

	// 快速排序
	int low = 0;
	int high = arr.length - 1;
	quickSort(arr, low, high);
	}

	public static void quickSort(int[] arr, int low, int high) {
	// 如果指针在同一位置 (只有一个数据时)，退出
	if (high - low < 1) {
	return;
	}
	// 标记，从高指针开始，还是低指针（默认高指针）
	boolean flag = true;
	// 记录指针的其实位置
	int start = low;
	int end = high;
	// 默认中间值为低指针的第一个值
	int midValue = arr[low];
	while (true) {
	// 高指针移动
	if (flag) {
	// 如果列表右方的数据大于中间值，则向左移动
	if (arr[high] > midValue) {
	high--;
	} else if (arr[high] < midValue) {
	// 如果小于，则覆盖最开始的低指针值，并且移动低指针，标志位改成从低指针开始移动
	arr[low] = arr[high];
	low++;
	flag = false;
	}
	} else {
	// 如果低指针数据小于中间值，则低指针向右移动
	if (arr[low] < midValue) {
	low++;
	} else if (arr[low] > midValue) {
	// 如果低指针的值大于中间值，则覆盖高指针停留时的数据，并向左移动高指针。切换为高指针移动
	arr[high] = arr[low];
	high--;
	flag = true;
	}
	}
	// 当两个指针的位置相同时，则找到了中间值的位置，并退出循环
	if (low == high) {
	arr[low] = midValue;
	break;
	}
	}
	// 然后出现有，中间值左边的小于中间值。右边的大于中间值。
	// 然后在对左右两边的列表在进行快速排序
	quickSort(arr, start, low -1);
	quickSort(arr, low + 1, end);
	}

# 7、堆排序（Heap Sort）

堆排序是一种 ** 选择排序，** 它的最坏，最好，平均时间复杂度均为 O (nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆分两种，父节点比子节点大的叫最大堆，父节点比子节点小的叫最小堆。

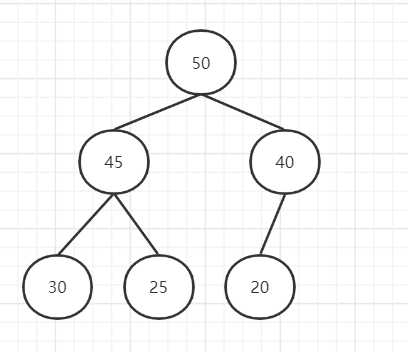
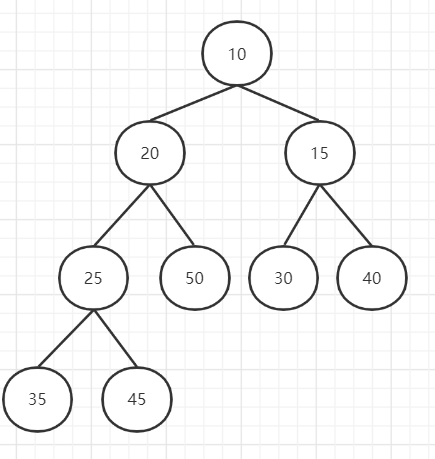
对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是

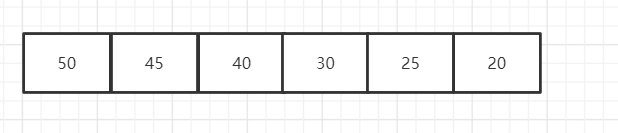
用公式描述：

大顶堆：arr [i] >= arr [2i+1] && arr [i] >= arr [2i+2]

小顶堆：arr [i] <= arr [2i+1] && arr [i] <= arr [2i+2]

升序采用大顶堆，降序采用小顶堆

eg: 最大顶堆：

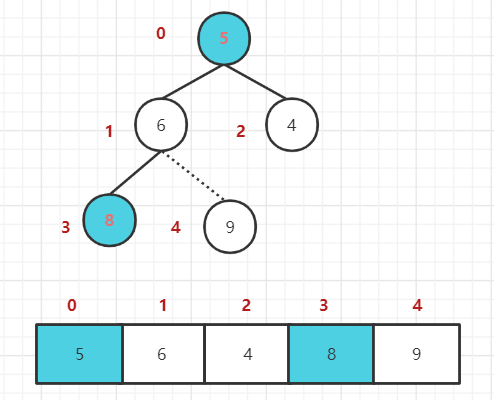
1. 初始结构如下：

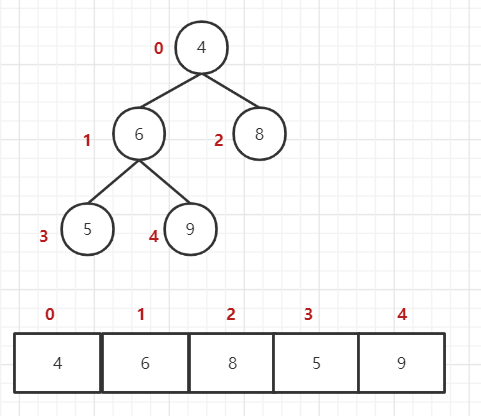
2. 最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的 6 结点），从左至右，从下至上进行调整。

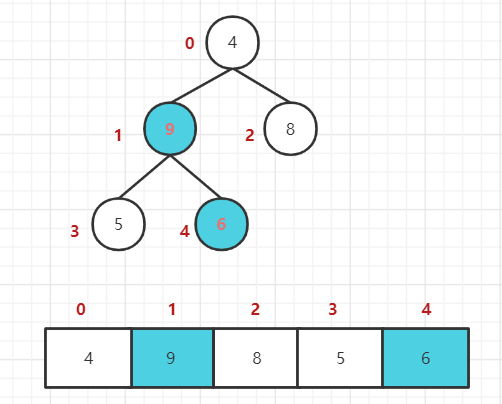
3. 找到第二个非叶节点 4，由于 [4,9,8] 中 9 元素最大，4 和 9 交换。

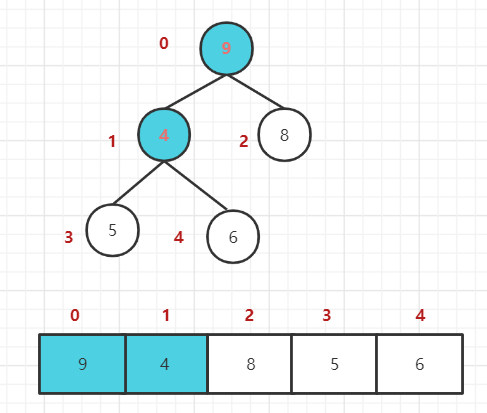
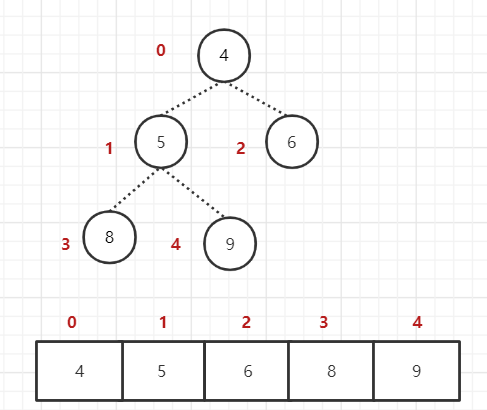
4. 子根 [4,5,6] 结构混乱，继续调整，[4,5,6] 中 6 最大，交换 4 和 6。

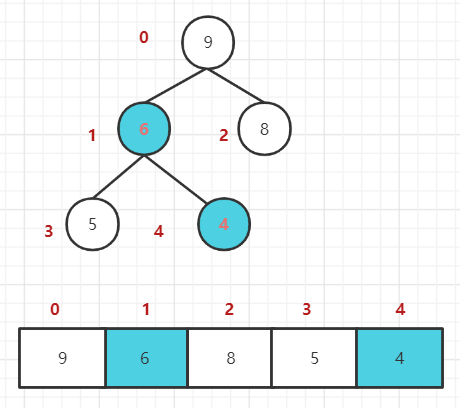
最小顶堆：将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

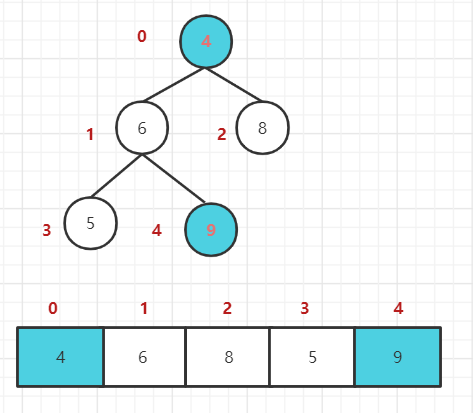
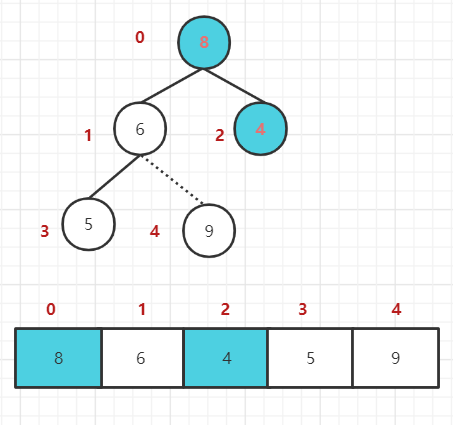
堆排序思路：

a. 将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆；

b. 将堆顶元素与末尾元素交换，将最大元素 "沉" 到数组末端；

c. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整 + 交换步骤，直到整个序列有序。

	import java.util.Arrays;

	/**
	* Created by chengxiao on 2016/12/17.
	* 堆排序 demo
	*/
	public class HeapSort {
	public static void main(String []args){
	int []arr = {9,8,7,6,5,4,3,2,1};
	sort(arr);
	System.out.println(Arrays.toString(arr));
	}
	public static void sort(int []arr){
	//1. 构建大顶堆
	for(int i=arr.length/2-1;i>=0;i--){
	// 从第一个非叶子结点从下至上，从右至左调整结构
	adjustHeap(arr,i,arr.length);
	}
	//2. 调整堆结构 + 交换堆顶元素与末尾元素
	for(int j=arr.length-1;j>0;j--){
	swap(arr,0,j);// 将堆顶元素与末尾元素进行交换
	adjustHeap(arr,0,j);// 重新对堆进行调整
	}

	}

	/**
	* 调整大顶堆（仅是调整过程，建立在大顶堆已构建的基础上）
	* @param arr
	* @param i
	* @param length
	*/
	public static void adjustHeap(int []arr,int i,int length){
	int temp = arr[i];// 先取出当前元素 i
	for(int k=i2+1;k<length;k=k2+1){// 从 i 结点的左子结点开始，也就是 2i+1 处开始
	if(k+1<length && arr[k]<arr[k+1]){// 如果左子结点小于右子结点，k 指向右子结点
	k++;
	}
	if(arr[k] >temp){// 如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
	arr[i] = arr[k];
	i = k;
	}else{
	break;
	}
	}
	arr[i] = temp;// 将 temp 值放到最终的位置
	}

	/**
	* 交换元素
	* @param arr
	* @param a
	* @param b
	*/
	public static void swap(int []arr,int a ,int b){
	int temp=arr[a];
	arr[a] = arr[b];
	arr[b] = temp;
	}
	}

# 8、计数排序（Counting Sort）

使用于有明确范围的数组：eg: 一个数组值的范围是 [n,m], 这个时候可以使用一个 m-n+1 长度的数组，待排序的数组就可以散在这个数组上，数组的值就是当前值的个数，然后散开得到的数组就有序了。

步骤：

获取数组的最大值和最小值；
遍历原数组，统计每一个元素出现的次数；
遍历计数数组，重新存入原数组，输出原数组即为排序后的数组；

原数组：

1. 计数数组长度：len = max -min +1=11-(-2) +1=14

2. 遍历原数组，统计个数，计数的角标 = 原数组元素 - min

代码实现：

	public class CountingSort {

	public static void main(String[] args) {
	int[] arr = { -2, 3, 5, 1, 7, 3, 11, 4 };
	sort(arr);
	}

	public static void sort(int[] arr) {
	int Max = arr[0];
	int Min = arr[0];
	for (int i = 0; i < arr.length; i++) {
	if (arr[i] > Max) {
	Max = arr[i];
	}
	if (arr[i] < Min) {
	Min = arr[i];
	}
	}

	int len = Max - Min + 1;
	int[] count = new int[len];
	for (int i = 0; i < arr.length; i++) {
	count[(arr[i] - Min)]++;
	}
	int h = 0;
	for (int m = 0; m < count.length; m++) {
	for (int j = 0; j < count[m]; j++) {
	arr[h] = m + Min;
	h++;
	}
	}

	for (int c = 0; c < arr.length; c++) {
	System.out.print(arr[c]+" ");
	}
	}

	}

# 9、桶排序（Bucket Sort）

桶排序顾名思义用桶对数据进行排序，但是我们需要十个桶，分别代表 0~9 这个十个数字。（借助这十个桶进行排序）

第一次进：按照所有数的个位数分类，分别把每个数放进对应数字的桶里。

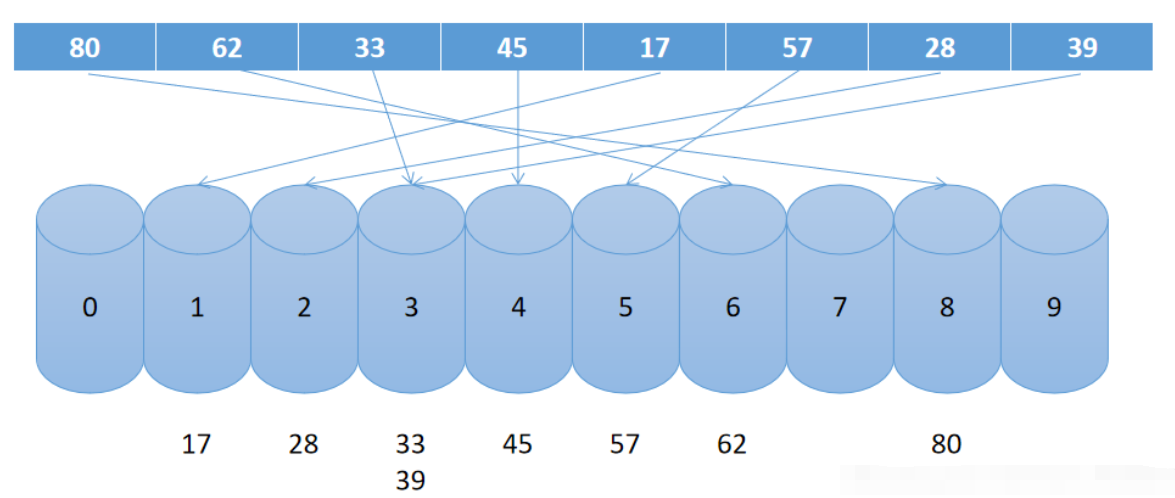
eg: 待排序的数为: 28，45，17，33，57，62，80，39，按其个位数分别放入对应的桶里，如下图所示：

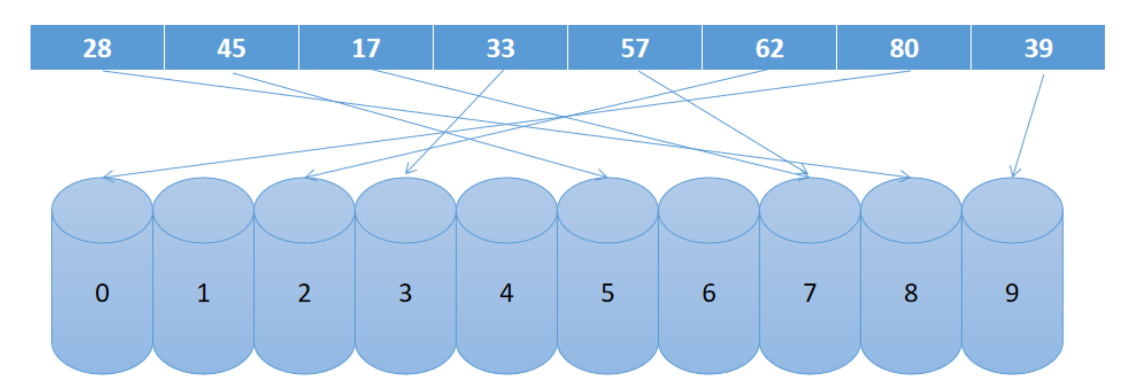
第一遍排序后十个桶里分别是：

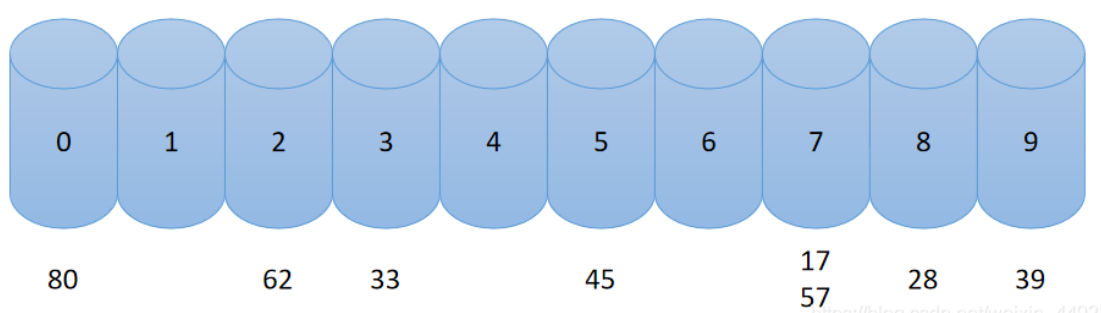
第一遍进桶后出桶，按从 0->9 的顺序重新存进数组里：
80,62,33,45,17,57,28,39

至此完成一进一出，由于该组数全部是两位数，所以整个排序过程需要两进两出，以此类推三位数需要完成三进三出。

第二遍进桶，按照其十位数字依次进桶：

二出：
17,28,33,39,45,57,62,80

至此，已完成该两位数数组的排序，若需排序的数组含有三位数，那么第三次进桶则按其百位数从 0->9 的顺序再依次进桶，后依次出桶。

	public static void bucketSort(int[] arr){

	// 计算最大值与最小值
	int max = Integer.MIN_VALUE;
	int min = Integer.MAX_VALUE;
	for(int i = 0; i < arr.length; i++){
	max = Math.max(max, arr[i]);
	min = Math.min(min, arr[i]);
	}

	// 计算桶的数量
	int bucketNum = (max - min) / arr.length + 1;
	ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
	for(int i = 0; i < bucketNum; i++){
	bucketArr.add(new ArrayList<Integer>());
	}

	// 将每个元素放入桶
	for(int i = 0; i < arr.length; i++){
	int num = (arr[i] - min) / (arr.length);
	bucketArr.get(num).add(arr[i]);
	}

	// 对每个桶进行排序
	for(int i = 0; i < bucketArr.size(); i++){
	Collections.sort(bucketArr.get(i));
	}

	// 将桶中的元素赋值到原序列
	int index = 0;
	for(int i = 0; i < bucketArr.size(); i++){
	for(int j = 0; j < bucketArr.get(i).size(); j++){
	arr[index++] = bucketArr.get(i).get(j);
	}
	}
	}

# 10、基数排序（Radix Sort）

桶排序的扩展：以整数排序为例，主要思想是将整数按位数划分，准备 10 个桶，代表 0 - 9，根据整数个位数字的数值将元素放入对应的桶中，之后按照输入赋值到原序列中，依次对十位、百位等进行同样的操作，最终就完成了排序的操作。

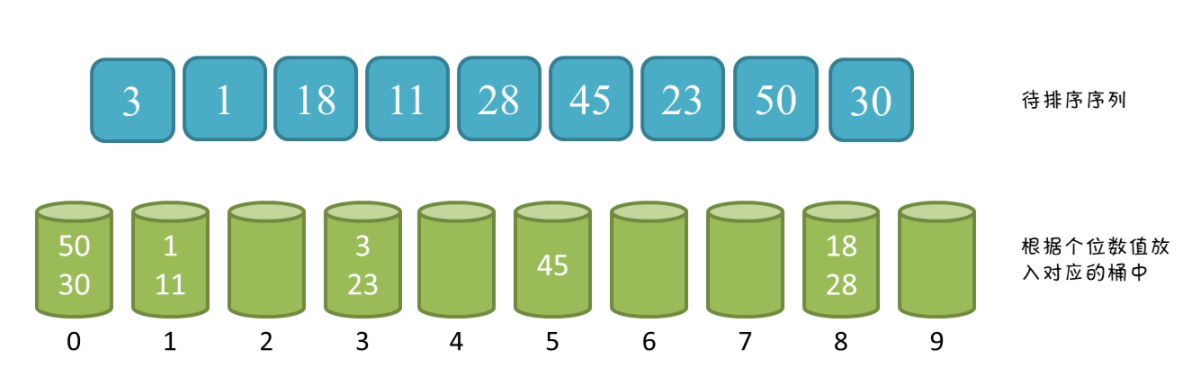
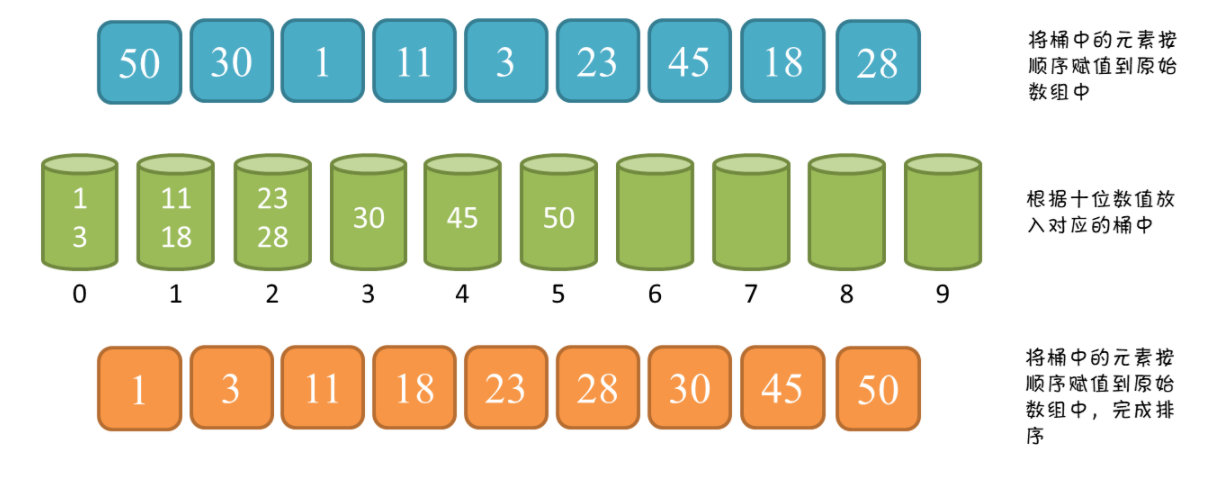
代码：

	// 基数排序
	public static void radixSort(int[] arr) {
	if (arr == null \|\| arr.length < 2) {
	return;
	}
	radixSort(arr, 0, arr.length - 1, maxbits(arr));
	}

	// 计算最大位数
	public static int maxbits(int[] arr) {
	int max = Integer.MIN_VALUE;
	for (int i = 0; i < arr.length; i++) {
	max = Math.max(max, arr[i]);
	}
	int res = 0;
	while (max != 0) {
	res++;
	max /= 10;
	}
	return res;
	}

	// 基数排序
	public static void radixSort(int[] arr, int begin, int end, int digit) {
	final int radix = 10;
	int i = 0, j = 0;
	int[] count = new int[radix];
	int[] bucket = new int[end - begin + 1];
	// 依次遍历每个位数
	for (int d = 1; d <= digit; d++) {
	for (i = 0; i < radix; i++) {
	count[i] = 0;
	}

	// 统计数量
	for (i = begin; i <= end; i++) {
	j = getDigit(arr[i], d);
	count[j]++;
	}

	// 计算位置
	for (i = 1; i < radix; i++) {
	count[i] = count[i] + count[i - 1];
	}

	// 记录到对应位置
	for (i = end; i >= begin; i--) {
	j = getDigit(arr[i], d);
	bucket[count[j] - 1] = arr[i];
	count[j]--;
	}
	for (i = begin, j = 0; i <= end; i++, j++) {
	arr[i] = bucket[j];
	}
	}
	}

	// 获取位数数值
	public static int getDigit(int x, int d) {
	return ((x / ((int) Math.pow(10, d - 1))) % 10);
	}

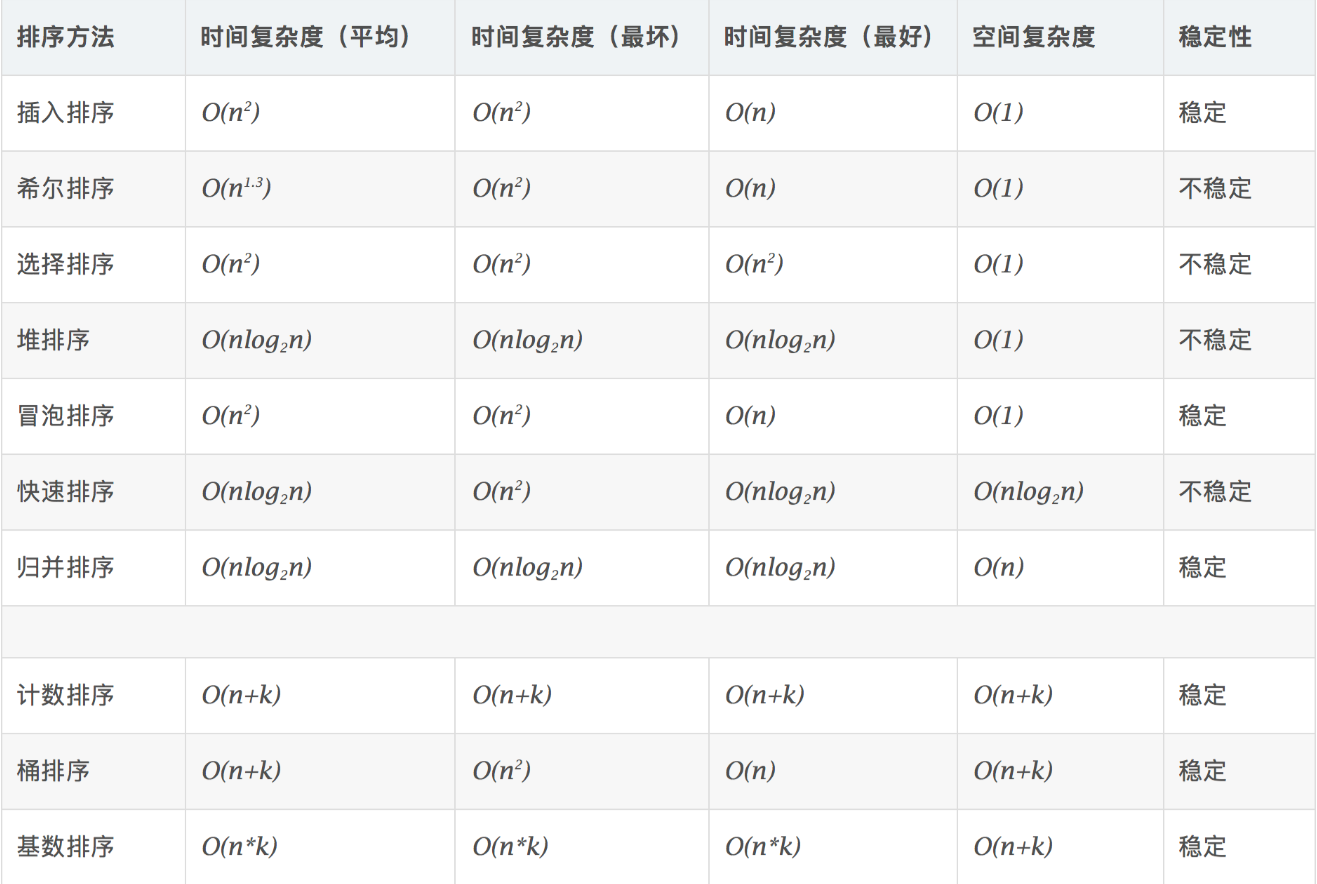
经常会问：查找一个元素，问快速排序第几次找到这个元素。

以及各个排序的时间复杂度。