力扣刷题笔记
# 1. 最后一个单词的长度 难易程度: 🌟
题目描述:给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s= "Hello World" | |
输出: 5 | |
解释:最后一个单词是“World”,长度为4。 |
示例 2:
输入:s = " fly me to the moon " | |
输出:4 | |
解释:最后一个单词是“moon”,长度为4。 |
tips:
1 <= s.length <= 104s仅有英文字母和空格' '组成s中至少存在一个单词
1. 暴力解法:直接使用 API
class Solution { | |
public int lengthOfLastWord(String s) { | |
// 注意提示 s 中至少存在一个单词,如果有一个单词直接返回 | |
if(s.length() == 1) return 1; | |
// 对 s 按照空格进行分割成字符串数组 | |
String[] str = s.split(" "); | |
// 得到数组最后一个字符串 | |
String last = str[str.length -1]; | |
// 返回这个字符串的长度 | |
return last.length(); | |
} | |
-----------分割线--------------------- | |
// 下面是别人的解法:可以学习和参考 | |
public int lengthOfLastWord(String s) { | |
s = s.trim(); | |
return s.length() - s.lastIndexOf(" ") - 1; | |
} | |
-----------官方解法----------------------- | |
public int lengthOfLastWord(String s) { | |
// 反向遍历字符串,寻找最后一个单词并计算其长度。 | |
int index = s.length() - 1; | |
while (s.charAt(index) == ' ') { | |
index--; | |
} | |
int wordLength = 0; | |
// 从最后一个字母开始继续反向遍历字符串,直到遇到空格或者到达字符串的起始位置。 | |
while (index >= 0 && s.charAt(index) != ' ') { | |
wordLength++; | |
index--; | |
} | |
return wordLength; | |
} | |
} |
# 2. 螺旋矩阵 II🌟🌟🌟
题目描述:给你一个正整数 n ,生成一个包含 1 到 n x n 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
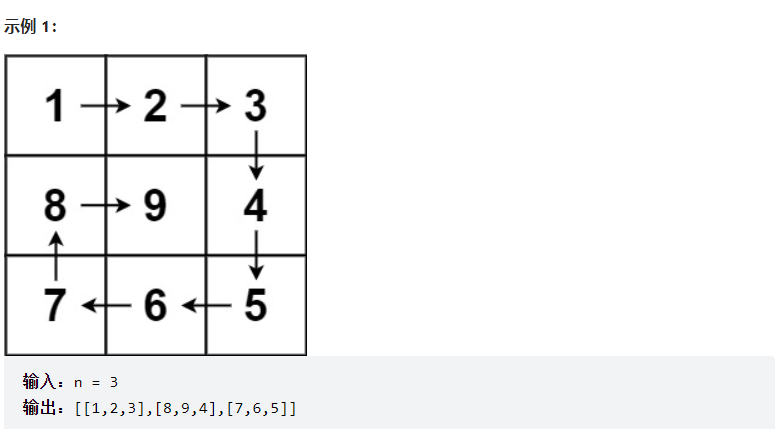
模拟这种层层循环:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
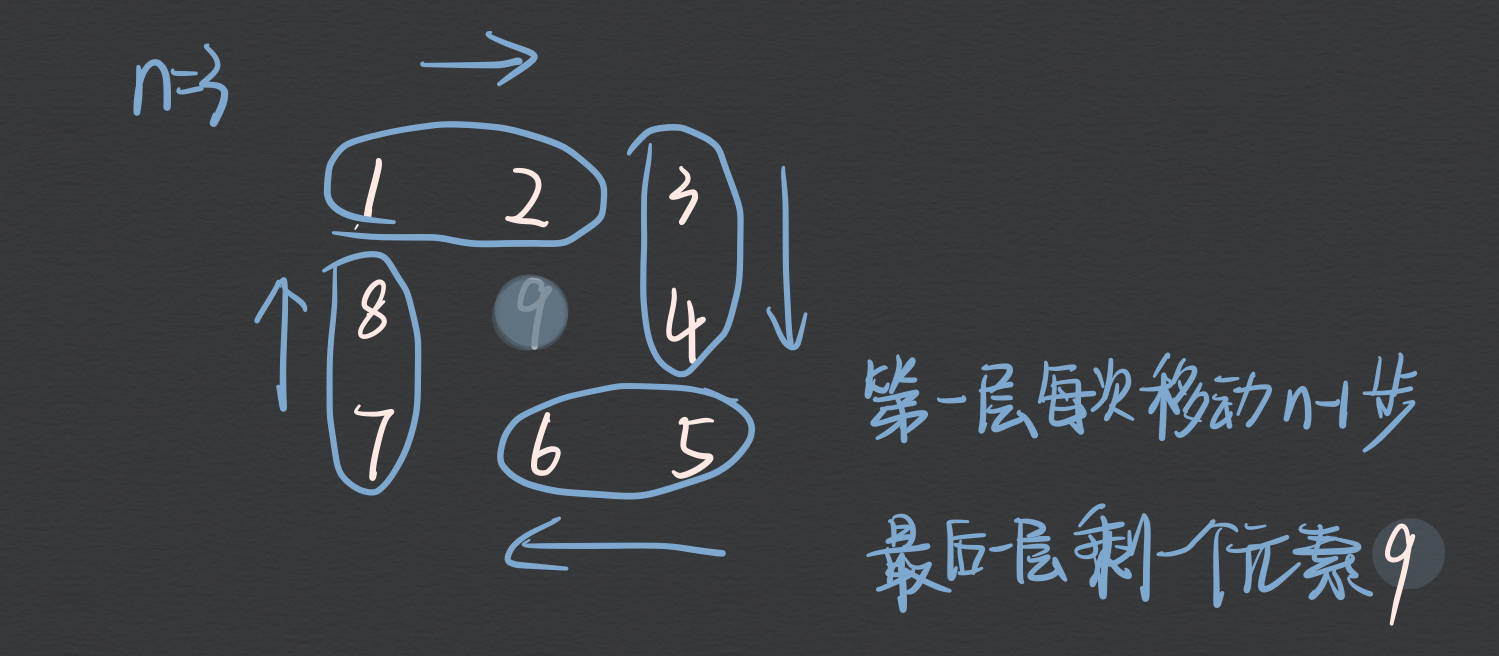
# 可以举例:n == 3 时:
1. 第一次循环四个方向:坐标每次移动 2 位
2. 还剩一个元素,不用再走四个方向上的移动
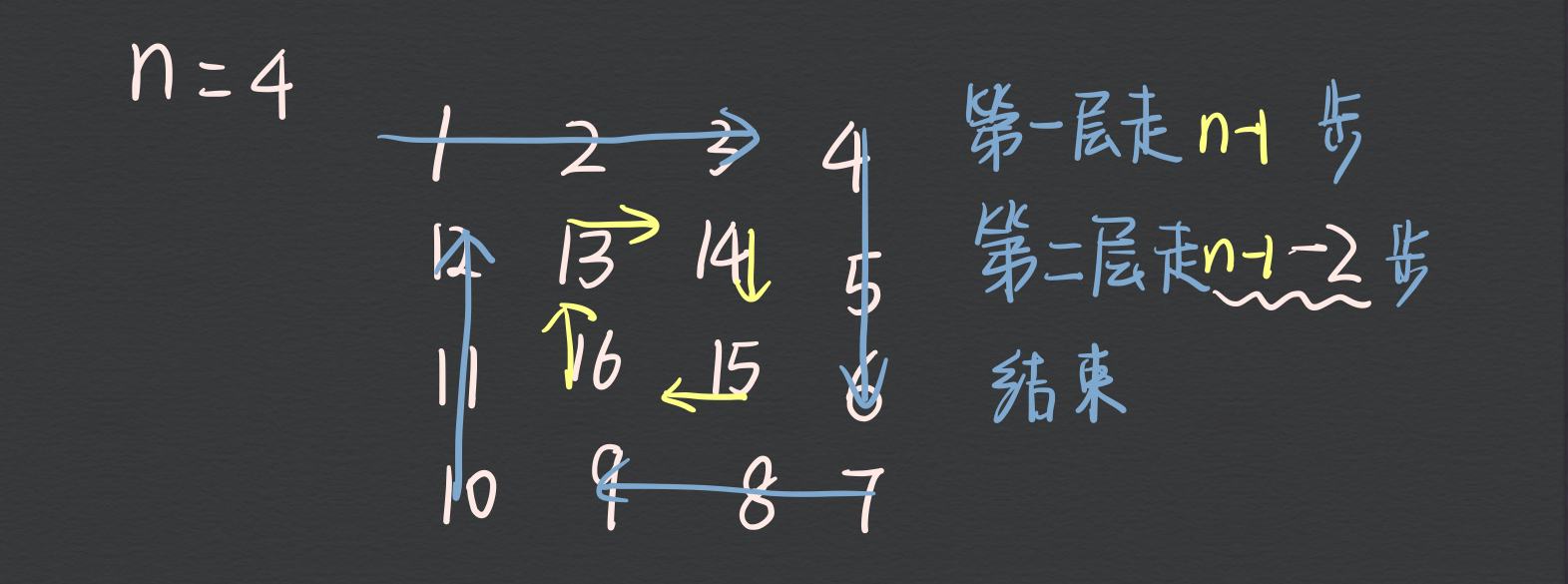
# n == 4 时:
1. 第一次循环走 3 步;
2. 第二次循环每次移动 1 步,是在 3 的基础上减去两条已经走过的边;
3. 循环结束,不剩余元素;
# n == 5 时:
1. 第一次循环走 4 步;
2. 第二次循环走 2 步,是在 4 的基础上减去两条已经走过的边;
3. 还剩一个元素,不用再走四个方向上的移动
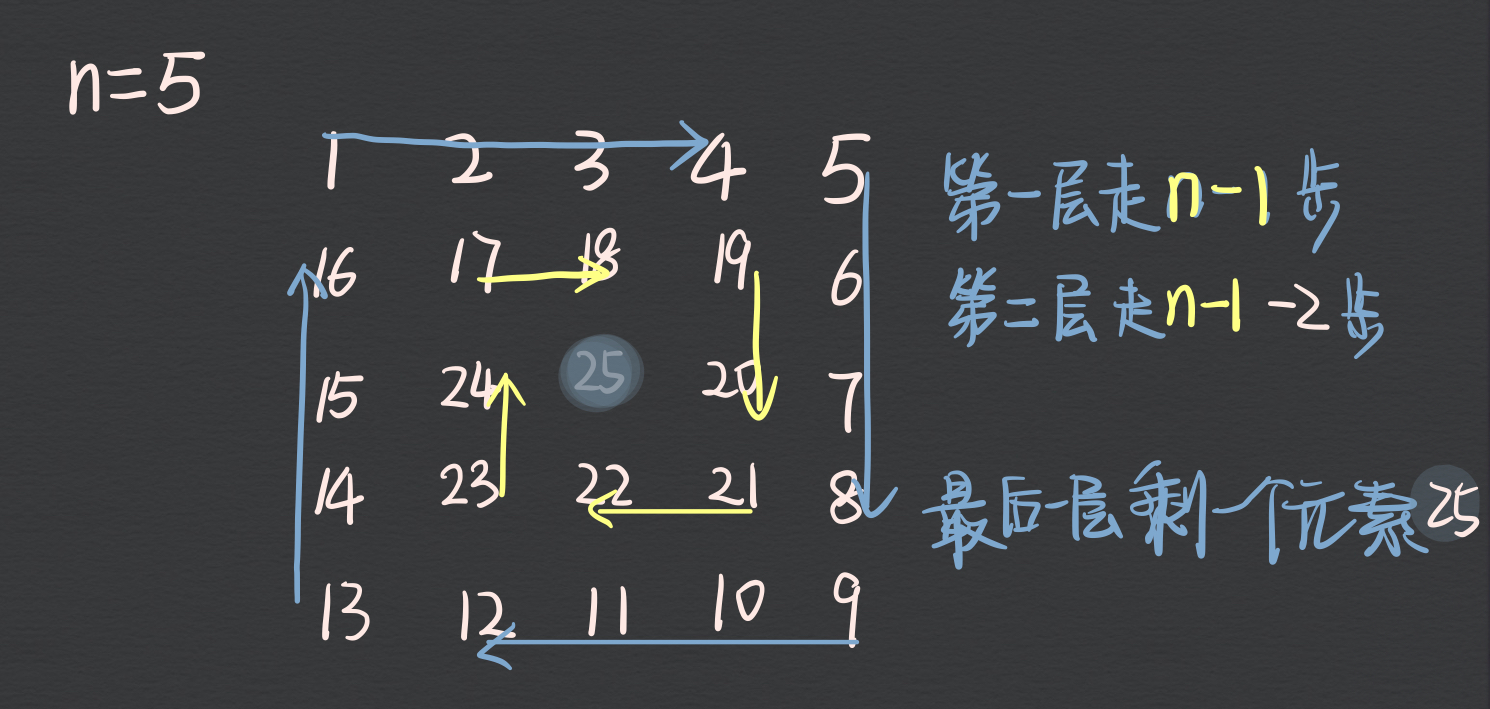
从上面的举例可以发现规律:
1.n 为奇数时,最里层总会剩下元素没有填充;
n 为偶数时,循环结束所有元素都被填充,不会额外剩下元素;
**2.** 第一层总是走 n-1 步;
第二层总是走上一次循环步数的基础上少 2;
class Solution { | |
public int[][] generateMatrix(int n) { | |
if(n == 1){ // 只有一个元素,直接返回 | |
return new int[][]<!--swig0-->; | |
} | |
int[][] matrix = new int[n][n]; | |
int num = 1; // 数字开始处 | |
int row = 0; // 行坐标 | |
int col = 0; // 列坐标 | |
int count = n /2; // 循环次数 | |
int step = n; // 一次走多少步,第一次为 n, 在循环里面改 step 的值 | |
while( count > 0 ){ | |
// 向左走 n-1 | |
for(int i = 0; i < step - 1;i++){ | |
matrix[row][col++] = num++; //row 不变 col++ | |
} | |
// 向下走 n-1 | |
for(int i = 0; i < step-1; i++){ | |
matrix[row++][col] = num++; //row++,col 不变 | |
} | |
// 向右走 n-1 | |
for(int i = 0; i < step -1;i++){ | |
matrix[row][col--] = num++; //row 不变 col-- | |
} | |
// 向上走 n-1 | |
for(int i = 0; i < step -1 ; i++){ | |
matrix[row--][col] = num++; //row--,col 不变 | |
} | |
step = step-2; // 下一次循环步数 | |
col++; // 列从新的循环位置开始 | |
row++; // 行从新的循环位置开始 | |
count --; // 循环次数减少 | |
} | |
// 如果 n 为奇数,还要再填充一位元素 | |
if(n % 2 == 1){ | |
matrix[row][col] = num; | |
} | |
return matrix; | |
} | |
} |
官方题解思路:之一
模拟矩阵的生成。按照要求,初始位置设为矩阵的左上角,初始方向设为向右。若下一步的位置超出矩阵边界,或者是之前访问过的位置,则顺时针旋转,进入下一个方向。如此反复直至填入 n2 个元素。
记 matrix 为生成的矩阵,其初始元素设为 0。由于填入的元素均为正数,我们可以判断当前位置的元素值,若不为 0,则说明已经访问过此位置。
class Solution { | |
public int[][] generateMatrix(int n) { | |
int maxNum = n * n; | |
int curNum = 1; | |
int[][] matrix = new int[n][n]; | |
int row = 0, column = 0; | |
int[][] directions = <!--swig1-->; // 右下左上 | |
int directionIndex = 0; | |
while (curNum <= maxNum) { | |
matrix[row][column] = curNum; | |
curNum++; | |
// 下一行,下一列的位置 | |
int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1]; | |
// 下一行列超出了 边界 n, 就旋转方向 | |
if (nextRow < 0 || nextRow >= n || nextColumn < 0 || nextColumn >= n || matrix[nextRow][nextColumn] != 0) { | |
directionIndex = (directionIndex + 1) % 4; // 顺时针旋转至下一个方向 | |
} | |
// 行和列位置移动 | |
row = row + directions[directionIndex][0]; | |
column = column + directions[directionIndex][1]; | |
} | |
return matrix; | |
} | |
} |
# 一定要会的 DFS
这是一套模板,很多地方都会用到这个思想
1. 从左上角开始移动,方向依次向右、向下、向左、向上、向右
2. 转向的条件是撞到墙:定义墙是:到达某边界 和 到达某遍历过的格子
3. 撞墙时,我们需要改变行走方向
class Solution { | |
// 定义移动方向,右,下,左,上 | |
public static int[] dx = {1, 0, -1, 0}; | |
public static int[] dy = {0, 1, 0, -1}; | |
// 定义行走方向 | |
int direction = 0; | |
// 定义返回结果 | |
public static int[][] res; | |
public int[][] generateMatrix(int n) { | |
// 初始化二维数组大小 | |
res = new int[n][n]; | |
dfs(n, 0, 0, 1); | |
return res; | |
} | |
// 深度优先搜索:递归 | |
public void dfs(int n, int x, int y, int num) { | |
// 判断条件:超出边界,或者遇到已经赋值过的方格 | |
if (x < 0 || x >= n || y < 0 || y >= n || res[y][x] != 0) { | |
// 撞到墙了,需要转向 | |
direction++; | |
// 如果已经转了一圈,需要从头开始如 dir = 4,需要再从 0 即向右移动 | |
direction %= 4; | |
return; | |
} | |
// 每次给该方格赋值 | |
res[y][x] = num; | |
// 循环供一次原方向,一次转向 | |
for (int i = 0; i < 2; i++) { | |
// 位移 | |
int mx = x + dx[direction]; | |
int my = y + dy[direction]; | |
// 递归下一个方格 | |
dfs(n, mx, my, num + 1); | |
} | |
} | |
} |
总结:1. 尽量少用现成 API;
2. 在第一次暴力求解的基础上,去考虑时间和空间优化问题;
3. 例如类似于第二个螺旋矩阵的题,可以使用 DFS 算法