力扣刷题笔记

# 1.DFS

约翰・霍普克洛夫特与罗伯特・塔扬在 1986 年共同获得计算机领域的最高奖：图灵奖。

深度优先搜索算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次.

下面通过题和联系去学会 DFS 方法。

下面是一般的 套路 ，不同情况不同处理。

	void dfs(int step) // 可能还有其他辅助参数，具体情况，具体处理
	{
	if(边界成立)
	{
	走到最深处
	。。。。。。
	return;
	}
	for(尝试每一种可能的状态)
	{
	if(如果这种状态可行){ // 剪枝
	把这种可能的状态标记，表示走过
	继续下一步dfs(step+1) // 状态转移
	把这种标记去除 // 回溯
	}
	}
	}

一般像求组合，求排列，三层循环以上就可以使用回溯算法了。

和递归一样，步骤：

1. 找到终止条件。（出口）

2. 确定单层循环逻辑。

你可以找找这些算法去练练手：

组合问题
77. 组合
216. 组合总数
17. 电话号码的字幕总和
分割问题
131. 分割回文串
93. 复原 IP 地址
子集问题
78. 子集
棋盘问题
51.N 皇后
37. 数独
其他问题
周围岛屿周长
// TODO...
后续有做到会继续更新这里。。。

# 1. 电话号码的字符组合难易程度: 🌟🌟🌟

题目描述：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

	输入：digits = "23"
	输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

	输入：digits = ""
	输出：[]

实例 3：

	输入：digits = "2"
	输出：["a","b","c"]

tips:

0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。

# 解法 1：

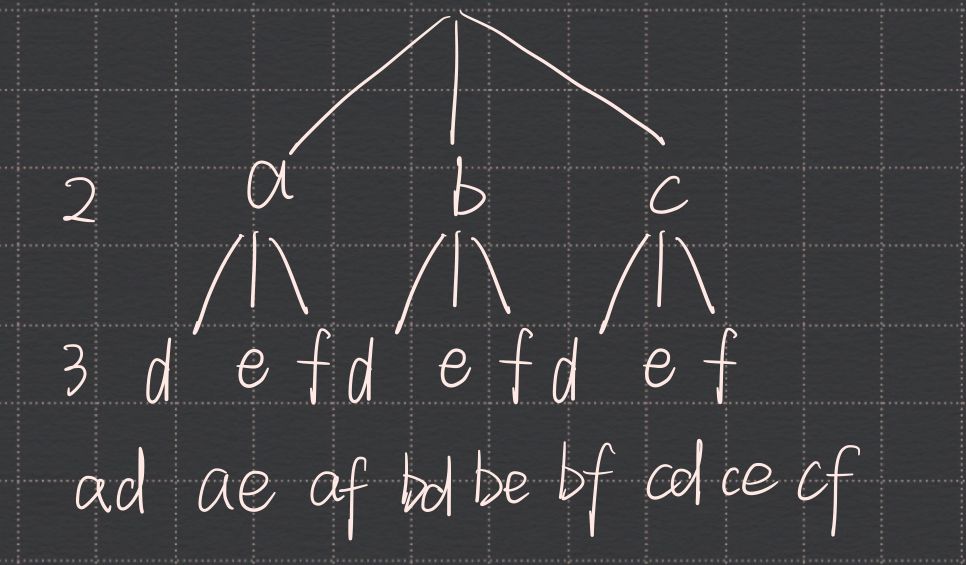
可以看出当 index == str.length () 时就截止了

	class Solution {
	char[][] letters = new char[][] {
	{}, // 0
	{}, // 1
	{'a','b','c'}, // 2
	{'d','e','f'}, // 3
	{'g','h','i'}, // 4
	{'j','k','l'}, // 5
	{'m','n','o'}, // 6
	{'p','q','r','s'}, // 7
	{'t','u','v'}, // 8
	{'w','x','y','z'} // 9
	};

	public List<String> letterCombinations(String digits) {
	List<String> res = new ArrayList<>();
	if(digits.length() == 0) return res;
	dfs(res, 0, new StringBuilder(), digits);
	return res;
	}

	void dfs(List<String> res,int index, StringBuilder sb, String str){
	// 截止条件
	if(index == str.length()){
	res.add(sb.toString());
	return ;
	}
	// 遍历一层的逻辑
	for(char c: letters[str.charAt(index) - '0']){
	sb.append(c);
	dfs(res, index+1, sb, str);
	sb.deleteCharAt(index);
	}
	}
	}

# 2. 组合总和🌟🌟🌟

题目：

给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

实例 1：

	输入：candidates = [2,3,6,7], target = 7
	输出：[[2,2,3],[7]]
	解释：
	2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
	7 也是一个候选， 7 = 7 。
	仅有这两种组合。

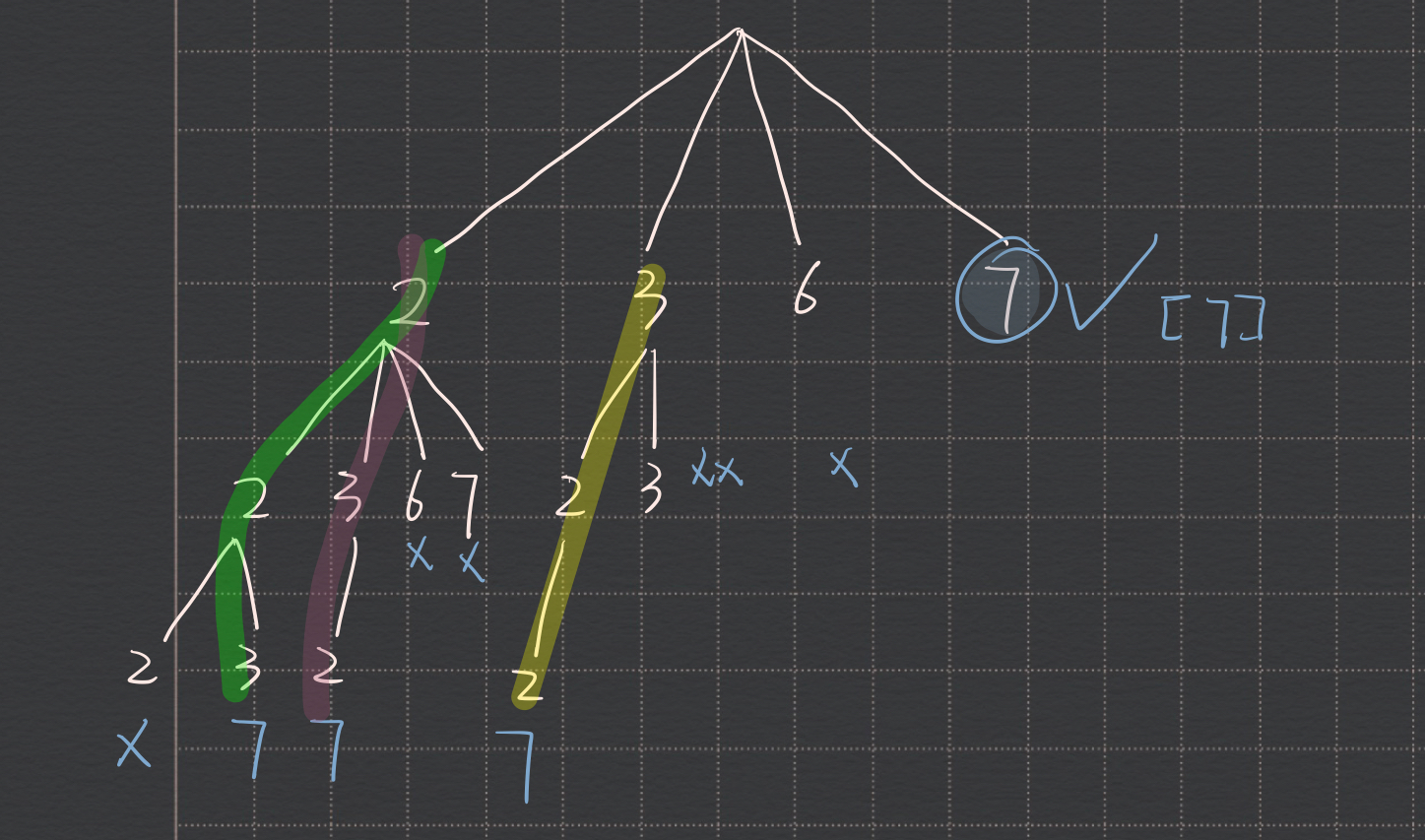
	class Solution {
	public List<List<Integer>> combinationSum(int[] candidates, int target) {
	List<List<Integer>> ans = new ArrayList<>();
	dfs(candidates, target, new ArrayList(), ans);
	return ans;
	}

	void dfs(int[] candidates, int target,List<Integer> li, List<List<Integer>> ans ){
	// 截止条件
	if(target <= 0){ // 剪枝
	if(target == 0){
	List<Integer> tmp = new ArrayList<>(li);
	Collections.sort(tmp);
	if(!ans.contains(tmp)){
	ans.add(tmp);
	}
	}
	return;
	}
	// 其他候选
	for(int i = 0; i < candidates.length; i++){
	li.add(candidates[i]);
	dfs(candidates, target-candidates[i], li, ans);
	li.remove(li.size() -1);
	}
	}
	}

# 3. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例一：

	输入：nums = [1,2,3]
	输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例二：

	输入：nums = [1]
	输出：[[1]]

代码：

	class Solution {

	public List<List<Integer>> permute(int[] nums) {

	List<List<Integer>> res = new ArrayList();
	boolean[] pb = new boolean[nums.length];
	dfs(nums, pb, new ArrayList(), res);
	return res;
	}

	private void dfs(int[] nums,boolean[] pb, List<Integer> li,List<List<Integer>> res){
	if(li.size() == nums.length){
	res.add(new ArrayList(li)); // 一定要注意这里 new ArrayList
	return;
	}
	for(int i = 0; i < nums.length; i++){
	if(!pb[i]){
	li.add(nums[i]);
	pb[i] = true;
	dfs(nums, pb, li, res);
	li.remove(li.size() -1);
	pb[i] = false;
	}
	}


	}
	}

数组, DFS

# 1.DFS

# 1. 电话号码的字符组合 难易程度: 🌟🌟🌟

# 解法 1：

# 2. 组合总和🌟🌟🌟

# 3. 全排列

Comparable&Comparator

SpringBootAdmin搭建

# 1. 电话号码的字符组合难易程度: 🌟🌟🌟