# 1. 将有序数组转成二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
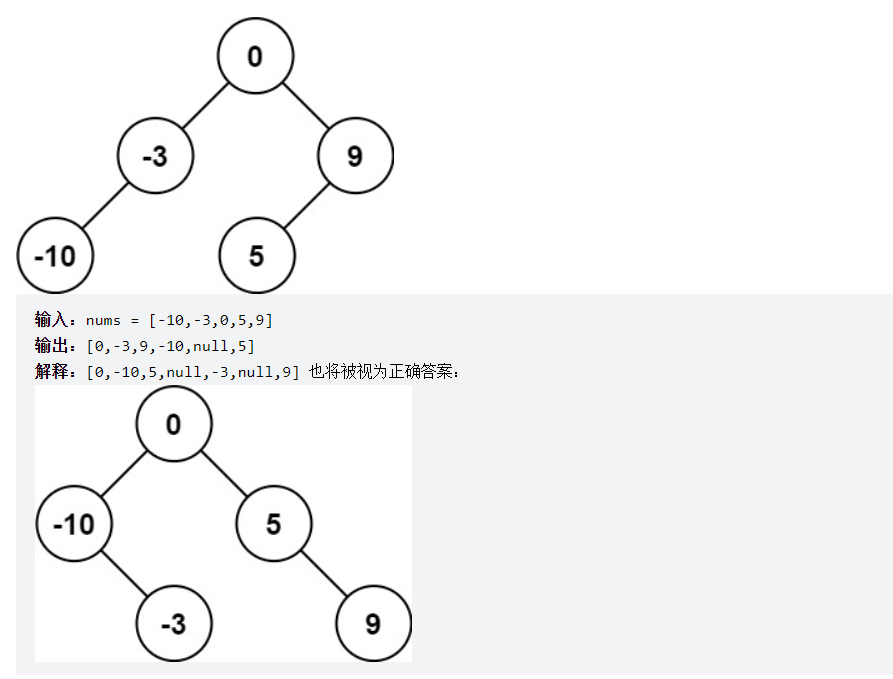
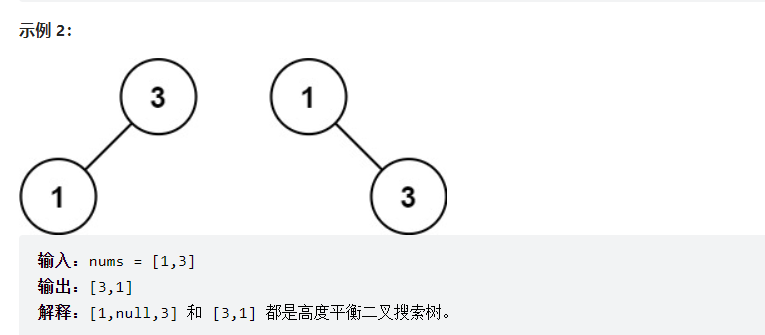
# 题解
在数组中选取一个元素为根节点,然后递归构造左右子树
注意:二叉搜索树的中序遍历是升序序列,题目中给的就是升序数组,因此可以确保是二叉树中的中序遍历序列。
# 1. 中序遍历:选择中间左边的数字作为根节点
class Solution { | |
public TreeNode sortedArrayToBST(int[] nums) { | |
return helper(nums, 0, nums.length - 1); | |
} | |
public TreeNode helper(int[] nums, int left, int right) { | |
if (left > right) { | |
return null; | |
} | |
// 总是选择中间位置左边的数字作为根节点 | |
int mid = (left + right) / 2; | |
TreeNode root = new TreeNode(nums[mid]); | |
root.left = helper(nums, left, mid - 1); | |
root.right = helper(nums, mid + 1, right); | |
return root; | |
} | |
} |
时间复杂度:O (N): 遍历一遍
空间复杂度:O (N), 开辟 N 个结点
# 2. 中序遍历:选择中间右边的数字作为根节点
class Solution { | |
public TreeNode sortedArrayToBST(int[] nums) { | |
return helper(nums, 0, nums.length - 1); | |
} | |
public TreeNode helper(int[] nums, int left, int right) { | |
if (left > right) { | |
return null; | |
} | |
// 总是选择中间位置右边的数字作为根节点 | |
int mid = (left + right + 1) / 2; | |
TreeNode root = new TreeNode(nums[mid]); | |
root.left = helper(nums, left, mid - 1); | |
root.right = helper(nums, mid + 1, right); | |
return root; | |
} | |
} |
# 3. 中序遍历:选择任意一个中间位置的数字作为根节点
class Solution { | |
Random rand = new Random(); | |
public TreeNode sortedArrayToBST(int[] nums) { | |
return helper(nums, 0, nums.length - 1); | |
} | |
public TreeNode helper(int[] nums, int left, int right) { | |
if (left > right) { | |
return null; | |
} | |
// 选择任意一个中间位置数字作为根节点 | |
int mid = (left + right + rand.nextInt(2)) / 2; | |
TreeNode root = new TreeNode(nums[mid]); | |
root.left = helper(nums, left, mid - 1); | |
root.right = helper(nums, mid + 1, right); | |
return root; | |
} | |
} |